Onze eerste Voxel – Maak een Minecraft-achtige Voxel wereld game in Unity #3

Welkom terug bij deel 3 van onze serie “Maak een Minecraft-achtig Voxel wereld game in Unity”! In deel 1 hebben we onze eerste 3D object gemaakt, een driehoek. Vandaag maken we onze eerste Voxel zo word onze wereld straks opgebouwd met meerdere Voxels.

Een Voxel (kubus) maken met code in Unity

Nu we weten hoe we een driehoek moeten maken, en we weten dat een vierkant uit 2 driehoeken bestaan kunnen we een vierkant maken. Met 6 vierkanten kunnen we vervolgens een Voxel (kubus) maken.

Onze eerste vierkant

Voor een driehoek hadden we 3 Vertices/Coordinaten aangemaakt. Voor het maken van onze 2e driehoek hebben we maar 1 extra Vertices nodig, want 2 Vertices kunnen we hergebruiken van de vorige driehoek zoals afgebeeld in de afbeelding.

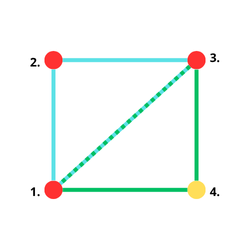
Zoals je in bovenstaande afbeelding ziet kan je door 1 extra Vertices toe te voegen een vierkant maken. Als we deze wijziging doorvoeren in onze code dan word onze Vertices array als volgt:

Vector3[] vertices = new[]
{
    new Vector3(0, 0, 0),
    new Vector3(0, 1, 0),
    new Vector3(1, 1, 0),
    new Vector3(1, 0, 0),
};

Zoals je misschien al was opgevallen hebben we de volgorde iets aangepast. Voor het maken van driehoeken (Faces) werken we namelijk met de klok mee, daarom is de nieuwe Vertices coordinaat toegevoegd als 1 na laatste item X-as 1 en Y-as 1.

Om de vierkant ook te tonen moeten we de face tekenen door de driehoek op te geven. Onze eerste driehoek waren de volgende indexes: 0, 1 en 2. Onze 2e driehoek zal bestaan uit 0, 2 en 3. Let op dit zijn de index in de Array, tel hier 1 bij op en je krijgt de hoek nummer van de afbeelding. Dus hoeknummers 1, 3 en 4.

int[] triangles = new[]
{
    0, 1, 2,
    0, 2, 3
};

Als we deze wijziging toepassen, en vervolgens op Play drukken in Unity zien we het volgende: een vierkant.

Hoe maken we nu een Voxel (kubus)?

Nu we een vierkant kunnen maken, zijn we toe aan het maken van een Voxel (kubus). In de vorige delen hebben we altijd 0 gebruikt voor de Z-as. Nu we de 3e dimensie in gaan word deze belangrijker.

Voor het maken van de achterkant van de Voxel (Kubus) hebben we de zelfde Vertices nodig maar dan 1 blok naar voren geschoven (van de camera af). Dit kunnen we dus bereiken door de Z-as op 1 te zetten voor deze 4 nieuwe vertices. Ook moeten we de volgorde omdraaien om de juiste richting de vierkant weer te geven.

Vector3[] vertices = new[]
{
    // Voorkant
    new Vector3(0, 0, 0),
    new Vector3(0, 1, 0),
    new Vector3(1, 1, 0),
    new Vector3(1, 0, 0),
    
    // Achterkant
    new Vector3(1, 0, 1),
    new Vector3(1, 1, 1),
    new Vector3(0, 1, 1),
    new Vector3(0, 0, 1),
};

Vervolgens moeten we dus weer 2 driehoeken maken tussen deze nieuwe Vertices. Dit zullen dus tussen de indexes 4, 5 en 6 zijn en vervolgens tussen 4, 6 en 7

int[] triangles = new[]
{
    // Voorkant
    0, 1, 2,
    0, 2, 3,
    
    // Achterkant
    4, 5, 6,
    4, 6, 7
};

Als we nu weer op Start drukken zien we nog steeds een vierkant, dit komt omdat de achterkant alleen zichtbaar is vanaf de andere kant. Als je naar de Scene view gaat en de andere kant bekijkt zul je zien dat daar ook een vierkant zichtbaar zal zijn.

Nu we onze voor en achter kant hebben gemaakt, kunnen we de linker en rechter zeide gaan maken. Hiervoor hebben we geen nieuwe Vertices meer voor nodig. Een Voxel (kubus) heeft namelijk 8 hoeken, deze 8 hoeken hebben we al opgegeven. Bij het maken van de linker en rechter kant moeten we nu ook rekening houden dat we de driehoek met de klok mee maken. Dit zullen voor de linker kant dus de indexes 7, 6, 1 en 7, 1, 0 zijn. Voor de rechter kant zal dit 5, 4, 3 en 5, 3, 2 zijn. dan zien onze triangles er als volgt uit:

int[] triangles = new[]
{
    // Voorkant
    0, 1, 2,
    0, 2, 3,
    
    // Achterkant
    4, 5, 6,
    4, 6, 7,
    
    // Linkerkant
    7, 6, 1,
    7, 1, 0,
    
    // Rechterkant
    5, 4, 3,
    5, 3, 2,
};

Nu we 4 zijdes van de 6 hebben gemaakt zijn we bijna klaar met onze Voxel (kubus). Als challenge wil ik dat je de laatste 2 zijdes compleet maak. Kom je er niet uit dan helpen we je graag verder in de comments. In de volgende post zullen we ook de volledige lijst van triangles geven mocht het je niet gelukt zijn.

Wat hebben we geleerd

• Hoe een vierkant is opgebouwd uit 2 driehoeken
• Dat driehoeken (Faces) altijd met de klok mee opgebouwd moeten worden
• Hoe je de Z-as gebruikt voor een 3D weergave
• Hoe je een Voxel (kubus) opbouwt met meerdere vierkanten

Volgende stap: Textures

In deel 4 gaan we beginnen met het weergeven van Textures op onze Voxel (kubus) zo zullen we onze eerste Dirt blok maken.
Klaar om de eerste dirt blok te maken? Tot de volgende keer!